🔢 Sistem Bilangan Real

📑 Topik

1. Bilangan Real
2. Nilai Mutlak
3. Grafik Persamaan
4. Grafik Persamaan Linear

📄 PDF Materi

Materi Bilangan Real dan Nilai Mutlak

🔢 Bilangan Real

ℹ️ Pengertian

Semua bilangan yang bisa ditulis dan memiliki nilai. Termasuk Bilangan positif dan negatif

Definisi bilangan lainnya :

• Bilangan Rasional adalah bilangan yang dapat di nyatakan sebagai $a/b$ dimana $b$ bukan 0.
• Bilangan Irasional adalah bilangan yang tidak dapat dinyatakan dalam bentuk $a/b$, Contoh : Bentuk $\sqrt{x}$, $\varphi$, $\log$

➕ Bilangan Positif dan Negatif

Pada garis koordinat , jika ada a dan b dua bilangan real, pasti memenuhi

1. $a\le b$
2. $a\ge b$
3. $a = b$

🚫 Teorema : Sifat Sifat Pertidaksamaan

Diberikan bilangan real p, q, r, dan s

1. jika $p < q$ dan $q < r$, maka $p < r$.
2. Jika $p < q$, maka $p + r < q + r$ dan $p - r < q - r$
3. Jika $p < q$, maka $pr < qr$ untuk $r > 0$, dan $pr > qr$ untuk $r < 0$
4. Jika $p < q$ dan $r < s$, maka $p + r < q + s$
5. Jika $p$ dan $q$ keduanya positif atau keduanya negatif, dan $p < q$, maka $1/p > 1/q$

trivia

Nilai 0 bukan bilangan positif atau negatif

📏 Selang pada Bilangan Real (Interval)

Jika $a$ dan $b$ bilangan real $a < b$,

1. Selang tertup dari $a$ ke $b$ ditulis dengan $[a,b]$

2. Selang terbuka yang dibatasi oleh $a$ dan $b$ ditulis dengan $(a,b)$

3. Selang tak hingga $(-\infty,b]$ dan $[a,+\infty)$ dipandang sebagai selang tertutup

   Karena semua titik di dalamnya termasuk titik ujung selang.

4. Sedangakan selang $(-\infty,b)$ dan $(a,+\infty)$ adalah selang terbuka

📋 Contoh Pertidaksamaan

1. Dapatkan penyelesaian dari $4+5x\le3x-7$, dengan menggunakan sifat-sifat pada teorema sebelumnya, untuk mengumpulkan $x$ pada satu sisi pertidaksamaan:

$5x\le 3x-11$
$2x\le -11$
$-x\le -11/2$

Jadi himpunan penyelesaiannya adalah $(-\infty,-11/2]$.

Ingat!

Penyelesain $x$ adalah Semua nilai $x$ yang mungkin untuk memenuhi persamaan

2. Selesaikan $\frac{2x-5}{x-2} < 1$

caution

Tidak diperkenankan mengali silang karena penyebutnya berupa variabel

$$\frac{2x-5}{x-2} -1 < 0\\ \frac{x-3}{x-2} < 0$$

Lalu uji nilai $x$, didapat $\{x | 2<x<3\}$

💪 Nilai Mutlak

Nilai mutlak adalah suatu bilangan real $a$, ditulis dengan mutlak a,didefinisikan dengan

$$|a| \ge 0 \rightarrow a\\ |a| \le 0 \rightarrow -a$$

📄 Contoh Nilai Mutlak

1. Selesaikan persamaan $|7x-4 = 2|$ Penyelesaian, berdasarkan definisi nilai mutlak, persamaan tersbut terdiri dari dua persamaan yaitu,
   • $7x -4 =2$ untuk $7x-4 \ge 0$
   • $-(7x-4) = 2$ untuk $7x-4 \le 0$

Penyelesaian untuk dua persamaan tersebut adalah $x=\frac{2}{7}$ dan $x=\frac{6}{7}$

2. Selesaikan persamaan $|3x-2|$ = $|5x +4|$

Penting!

2 Mutlak memuat 4 Kemungkinan

Didapat $x=3$

🪢 Hubungan Nlai mutlak dengan Nilai akar

untuk setiap bilangan real $a$, berlaku

$$\sqrt{a^2}=|a|$$

🏷️ Sifat dasar Nilai Mutlak

1. $|p| \ge 0$
2. $|p|=|-p|$
3. $|pq|=|p||q|$
4. $|p/q| = \frac{p}{q}$

📍 Rumus Jarak

Jika terdapat dua titik $P$ dan $Q$, jarak antara titik p dan q adalah :

$$d=|q-p|$$

Contoh

1. $|2x-3|<6$

• kemungkiann 1

$$2x-3<6\\ x < 9/2$$

Lalu uji syarat $2x-3\ge0$ didapat $3/2$
dan uji titik didapat serta dinyatakan dalam $\{x|3/2\le x<9/2\}$

• Kemungkinan 2

$$-(2x-3)<6\\ x > -3/2$$

Lalu diuji syarat $2x-3<0$ didapat $x<3/2$
solusi $\{x|-3/2<x<3/2\}$

2. $|x-6|=x-6$ Jawaban untuk persamaan ini bisa langusung menjadi $x-6\ge0$ karena menurut teori $|x|=x$.

Catatan

Penyelesain dari $x$ menggunakan garis bilangan

Trivia

$|x^2|=x^2$ hanya memiliki satu kemungkinan , yaitu selalu positif

📈 Grafik

Grafik suatu persamaan yang menghubungkan dua peubah $x$ dan $y$ adalah himpunan semua titik pada bidang-$xy$ yang koordinatnya merupakan anggota himpunan penyelesaian persamaan tersebut

📊 Kurva Dasar

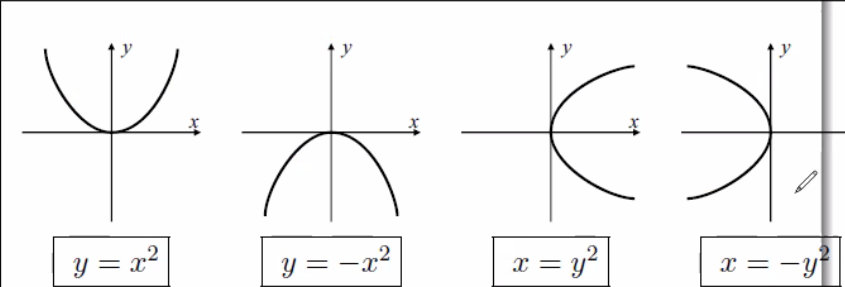
✏️ Latihan Soal

Cara Pengerjaan

1. Mensubtitusi koordinat ke dalam persamaan
2. subtitusikan $-y$ ke variabel $y$ di persamaan, jika persamaan berubah maka persamaan tersebut tidak simetris dengan sumbu x

Catatan

Ciri ciri simetris terhadap sumbu $x$ adalah jika variabel $y$ berpangkat genap

📏 Kemiringan Garis

Misal $P(x_1,y_1)$ dan $Q(x_2,y_2)$ Kemiriingan garis yang melalui P dan Q didefinisikan dengan

$$m=\frac{y_2-y_1}{x_2-x_1}$$

Kemiringan suatu garis dari dua titik dapat menggunakan sembarang titik berada di garis tersebut. Dengan rumus

$$\frac{y_1-y_2}{x_1-x_2}=\frac{y-y_1}{x-x_1}$$

✏️ Contoh Kemiringan Garis

Dapatkan kemiringan garis melalui

1. titik $(2,3)$ dan $(4,6)$
2. titik $(2,9)$ dan $(4.3)$
3. titik $(-2,7)$ dan $(5,7)$

Tips

rumus gradien dipersingkat menjadi

$$m=\frac{\Delta y}{\Delta x}$$

Penting

Nilai gradien nol artinya garis tersebut sejajar dengan sumbu x, jika sejajar dengan sumbu y maka gradiennya tak terdefiniskan

Gradien persamaan umum

Gradien untuk $ax+by+c=0$ adalah $m=\frac{-a}{b}$

🔘 Sudut Kemiringan

Sudut kemiringan garis $l$ adalah sudut $\varphi$ terkecil yang diukur berlawanan arah jarum jam dari arah sumbu-$x$ positif ke garis $l$

$$\varphi=\arctan m$$

🪢 Hubungan Antara Dua Garis

Jika garis $l_1$ mempunyai kemiringan $m_1$ dan garis $l_2$ memupunyai kemiringan $m_2$, maka

1. $l_1$ sejajar $l_2$ jika dan hanya $m_1=m_2$
2. $l_1$ tegak lurus terhadap $l_2$ jika dan hanya jika $m_1m_2=-1$

➖ Bentuk bentuk persamaan garis

1. $\boxed{\frac{y-y_1}{x-x_1}=\frac{y_2-y_1}{x_2-x_1}}$

2. $\boxed{y-y_1=m(x-x_1)}$

3. $\boxed{y=ax+b}$

4. $\boxed{x=a}$

5. $\boxed{y=b}$

✏️ Contoh Bentuk persamaan garis

Tentukan Persamaan garis dengan syarat syarat yang disebutkan dengan

1. dengan kemiringan $-9$ dan memotong sumbu $y$ di $(0,-4)$
2. dengan kemiringan $-1$ dan melalui titik pusat
3. melalui $(5,-1)$ dan tegak lurus terhadap $y-3x+4$
4. melalui $(3,4)$ dan $(2,5)$